PRINSIP-PRINSIP ASAS SISTEM STADIA

 

Dalam sistem ini didapati bahawa:                                                                                                         

Di atas gegendang pada alat ukur seperti tiodolit, alat aras, dan lain-lain, ditanda dengan 2 garisan ufuk tambahan yang dikenali sebagai garis-garis stadia.                                                             

Garis-garis stadia ini ditempatkan secara bertentangan dan sama jarak  di atas dan bawah bebenang tengah atau garisan tengah.                                                                                                 

Jarak diantara garisan-garisan stadia dinamakan sela stadia.                                                             

Sistem Stadia Tetap:                                                                                                                                        Garisan-garisan stadia atau sela stadia ditetapkan pada suatu kedudukan tertentu pada gegendang.                                                                                                                                                

Sistem Stadia Tidak Tetap:                                                                                                                                                                                                                                     Garisan-garisan stadia atau sela stadia boleh diubah kedudukannya  dan jarak sela stadia ini perlu diukur dengan menggunakan jangka halus.                                                                                        
Sistem stadia  jarang digunakan dalam kerja ukur sekarang kerana tidak tersedia atau  tidak   mempunyai kelebihan yang istimewa dan juga tidak mempunyai kejituan yang lebih tinggi

 

       

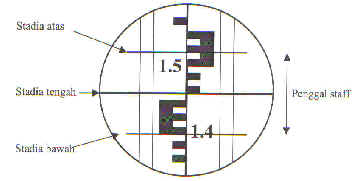
                                                                             Rajah 1

                                      
Cerapan-cerapan tekimeter dilakukan kepada suatu staf aras yang merupakan tapak yang tidak tetap nilainya.                                                                                                                                 
Apabila ditenung melalui teropong, akan didapati bahawa garis-garis stadia membentuk suatu nilai panjang yang tertentu bagi staf aras, di mana ukuran panjang ini akan bertambah besar nilainya apabila  kedudukan staf semakin jauh ditempatkan.
                                                                        
Ukuran panjang bagi staf ini dinamakan penggal staf. Ia berkadar terus dengan jarak bagi kedudukan alat ukur.                                                                                                                                                                   

Dengan menggunakan panjang penggal staf ini dalam pengiraan, maka jarak antara staf dan tekimeter boleh diperolehi.      

   





                                                                      Rajah 2

                                                        

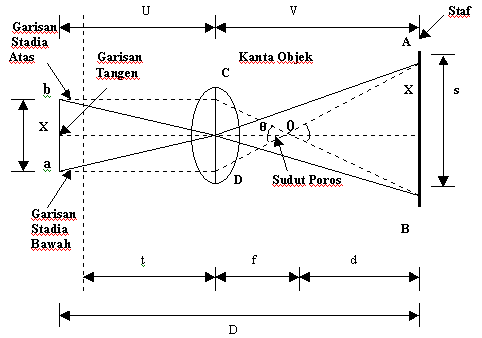                                                                    Rajah 3

 
Di mana;

 

        i     =    sela stadia ab, iaitu jarak sebenar di antara garisan-garisan stadia pada gegendang.

        t    =     jarak antara kanta objek dan paksi pugak.

       f    =     jarak fokus bagi kanta

      p    =     titik fokus luar bagi kanta objek

      O   =     jarak ufuk di antara titik fokus luar dan staf.

      D   =     jarak ufuk yang dikehendaki.

      s    =     penggal staf AB

     U    =     jarak di antara garisan-garisan stadia dengan kanta objek

     V    =     jarak di antara staf dengan kanta objek.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                        
Apabila diteropong sekali lagi, dalam keadaan supaya memberikan imej sama sekali, arca bagi staf AB akan terbentuk di ab pada satah gegendang. (sila rujuk pada rajah 2 dan 3 di atas)                                                                                  
Satu pancaran cahaya dari A akan melintas melalui O dan dengan melalui kanta objek, pancaran cahaya ini akan muncul selari dengan paksi optik. Serupa juga seperti yang berlaku pada pancaran cahaya dari B.                                                                                                                                                
Pancaran-pancaran cahaya yang dipertimbangkan akan membentuk dua buah segitiga sebentuk dan masing-masing dengan porosnya di O.                                                                                                                                                   
Selain daripada itu, tapak bagi segitiga yang lebih kecil yang berada di kanta objek akan mempunyai nilai yang sama dengan sela stadia, i.                                                                                                                                                                                           
Daripada segitiga-segitiga sebentuk COD dan AOB (sila rujuk rajah 3 di atas) didapati bahawa:

        s/d    =    i/f

        d/i    =    s/f

        d        =    sf/i

        tetapi f dan i adalah pemalar, oleh itu:

        d       =    Ks         maka;         K    =    f/i

        didapati bahawa;    D     =    d + f + t

        maka                      D     =    Ks + f + t

                                           =     Ks + (f + t)

        tetapi, f dan t juga ialah pemalar, maka;

        d     =    Ks + C

        C     =    f + t    (pemalar 'additive')

        biasanya,     K     =    100    dan C    =     0,

        maka,     D     =    100 s

        di mana s ialah bacaan penggal staf.