LUAS YANG DITUTUPI OLEH GARISAN TIDAK SEKATA

LUAS YANG DITUTUPI OLEH GARISAN TIDAK SEKATA

Bagi kes seperti ini,hanya keputusan terhampir sahaja yang boleh diperolehi.
Walaubagaimanapun,kaedah-kaedah yang diamalkan akan memberikan penghampiran yang terbaik.

GARISAN TOLAK ANSUR

Generalisasi telah dibuat ke atas rajah asal bagi membolehkan kiraan dibuat dengan kaedah Sisi Lurus seperti berikut:


                                                 Rajah 1

Rajah sisi yang tidak sekata dibahagikan kepada segitiga-segitiga atau trapezoid.
Sempadan tidak sekata digantikan dengan garis lurus.
Sebarang luas kawasan kecil yang terkeluar daripada pengukuran diimbangi oleh luas kawasan kecil pengukuran lain yang berada di luar garis yang sama.

(sila rujuk rajah 1 di atas)

KAEDAH MATEMATIK

       PERATURAN TRAPEZOID


                       Rajah 2a                                           Rajah 2b


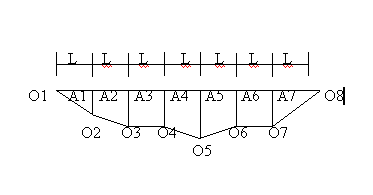
                                          Rajah 2C

A₁ = [ ( O₁ + O₂) / 2 ] L , A₂ = [ ( O₂ + O₃ ) / 2 ] L dan sebagainya

Oleh itu, untuk ofset N, jumlah luas (A) diberikan oleh:

A = [ ( O₁ + O₂ ) / 2 ] L + [ ( O2 + O3 ) / 2 ] L + .... + [ ( O_N-1 + O_N ) / 2 ] L

Peraturan di atas membawa pada peraturan trapezoid umum seperti yang ditunjukkan di bawah:

A = L [ O₁ + O_N + 2 ( O₂ + O₃ + O₄ +.......+ O_N-1 ) ]
2
Peraturan trapezoid ini boleh digunakan bagi sebarang bilangan ofset.

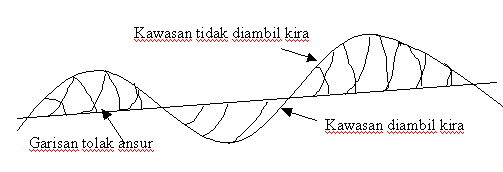
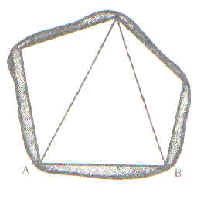
Berpandukan kepada Rajah 2a ia menunjukkan jaringan kawalan berada di sebelah dalam sebuah kawasan yang mempunyai sisi tidak sekata.

Kawasan lorek adalah baki yang akan dihitung selepas menggunakan satu daripada kaedah sisi lurus untuk menghitung luas yang ditutupi dengan garis-garis jaringan kawalan.

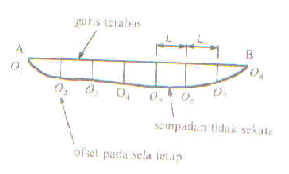
Rajah 2b menunjukkan pembesaran satu bahagian daripada Rajah 2a
Ofset-ofset O₁, O₂, O₃, dan seterusnya, sama ada diukur secara langsung di lapangan atau diskalakan daripada pelan.

Peraturan trapezoid mengandaikan bahawa jika sela antara ofset-ofset itu kecil, sempadan tersebut boleh dikira sebagai garis lurus antara ofset-ofset.

Oleh itu, Rajah 2b diandaikan terdiri daripada satu siri trapezoid seperti yang ditunjukkan dalam Rajah 2c.

PERATURAN SIMPSON


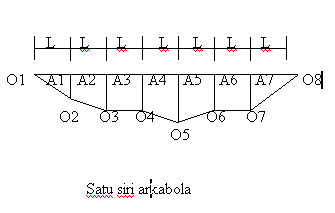
                                         Rajah 3

Kaedah ini terdiri daripada suatu siri arka parabola, bukannya terdiri daripada satu siri garis lurus.

Keputusan yang lebih tepat boleh didapati kerana penghampiran bentuk sebenar bagi sempadan tidak sekata yang lebih baik diperolehi.

Rajah 3 di bawah menunjukkan penghampiran ini digunakan bagi Rajah 2c di atas.

Peraturan Simpson mengandaikan ofset-ofset itu dalam beberapa set segitiga dan ia boleh ditunjukkan bahawa luas antara ofset 1 dan 3 diberikan oleh:

A₁ + A₂ = L ( O₁ + 4O₂+ O₃ )
             3

Begitu juga,

A3 + A4 = L ( O₃ + 4O₄ + O₅ )
             3

Oleh itu, secara umum

Jumlah luas = L ( O₁ + O_N + 4S ofset-ofset genap + 2S ofset-ofset ganjil )
                 3

Walaubagaimanapun, untuk menggunakan peraturan Simpson, N mesti bernombor ganjil.
Apabila bertemu dengan ofset-ofset genap seperti yang ditunjukkan dalam rajah 3 di atas, ofset terakhir mesti diabaikan (contohnya dalam rajah 3 di atas, O₈).
Luas dari O₁ hingga O₇ dikira dengan menggunakan peraturan Simpson dan luas kecil terakhir dikira sebagai satu trapezium (iaitu dengan menggunakan peraturan trapezoid).
Perhatikan contoh yang diberiokan semasa menerbitkan peraturan trapezoid diselesaikan dengan menggunakan peraturan Simpson.

KAEDAH GRAFIK

Kaedah ini melibatkan penggunaan kertas.
Grid lutsinar yang diletakkan (ditindihkan) di atas pelan terbabit.
Bilangan segiempat sama atau sebahagian daripadanya yang menutupi kawasan dikira, dan dengan mengetahui skala pelan,luas yang dihasilkan oleh segiempat sama diketahui dan jumlah luas boleh dihitung.
Kaedah ini akan menjadi lebih tepat jika grid kecil digunakan.

PENGGUNAAN ALAT PLANIMETER

Planimeter adalah alat mekanikal yang digunakan untuk menentukan luas bagi sebarang rajah satah sisi tidak sekata.
Melalui penggunaan alat ini darjah ketepatan yang tinggi mampu dicapai.
Luas diperolehi dari unit pengukuran yang terdiri daripada cakera kamiran.
Unit ini berpusing dan menukar bacaan apabila titik surih bergerak mengelilingi perimeter rajah. Unit ini boleh dibaca sehingga 1/1000 pusingan cakera.
Bacaan tersebut berhubung terus dengan panjang lengan surih.
Pada alat lengan surih tetap, bacaan diperolehi terus dalam unit mm².
Kemudian, terpaksa ditukarkan mengikut skala pelan untuk mendapatkan luas di atas tanah.
Pada alat lengan surih bergerak, panjang lengan surih boleh disetkan pada nilai-nilai tertentu dan ini bergantung pada skala pelan.
Bacaan-bacaan yang didapati memberikan luas di atas tanah secara terus.
Planimeter boleh digunakan seperti yang ditunjukkan dalam rajah 4a dan 4b di bawah.


                                  Rajah 4a: Ciri-ciri Utama Planimeter


                                     Rajah 4b: unit kamiran

Blok kutub berada di luar rajah :

Ini adalah kaedah yang biasa digunakan dan ditunjukkan dalam Rajah 4c di bawah.

Rajah 4c

Titik A ditandakan dan bacaan di unit pengukuran dicatatkan.
Titik surih digerakkan mengikut pusingan jam mengelilingi perimeter rajah dan balik semula ke titik A. Sekali lagi, unit pengukuran dibaca.
Perbezaan antara kedua-dua bacaan didarabkan dengan faktor tertentu untuk memberikan luas di atas tanah.
Blok kutub berada di dalam rajah:

Pada dasarnya, kaedah ini sama seperti blok kutub berada di luar rajah tetapi pemalar mesti ditambah seperti yang ditunjukkan di dalam Rajah 4d di bawah.

Rajah 4d
Kawasan berlorek dinamakan bulatan sifar dan luas ini tidak didaftarkan pada unit pengukuran disebabkan oleh cakera diheret bersudut tepat pada arah putaran semasa pengukuran.
Pemalar ini disertakan bersama planimeter dan harus ditukarkan apabila perlu.