ISIPADU ANTARA KERATAN RENTAS

KAEDAH PRISMOID

• Kaedah ini sama dengan kaedah mencari keluasan dengan menggunakan Peraturan Simpson dan biasanya lebih tepat daripada kaedah Keluasan Hujung.
  

• Isipadu yang dikira merupakan isipadu yang terkandung antara siri keratan rentas yang mempunyai jarak yang sama.
  

• Prismoid adalah rajah yang pejal dengan satah-satah hujung berkeadaan selari dan satah-satah sisi juga selari.
  

• Formula Prismoid boleh digunakan untuk kerja tanah bagi potongan dan tambakan dan memberikan isipadu sebenar sama ada:
  
  Cerun Lintang yang bersudut tepat pada garis tengah adalah lurus dan profil membujur pada garis tengah adalah berbentuk parabola
  
  Atau
  
  Cerun Lintang berbentuk parabola dan profil membujur adalah garis lurus.
  
  
  
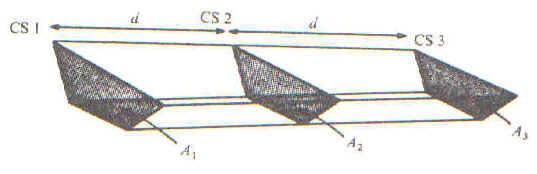
                                                              Rajah 1
  
  

• Untuk semua rumus di bawah, sila rujuk Rajah 1 di atas.
  

• Untuk siri segitiga keratan rentas, isipadu V _1-3 yang terkandung antara keratan rentas itu diberi oleh;
  

• V_1-3   =    d  ( A₁  +  4A₂  +  A₃ )
               3
  
  
  Jika rajah di atas dipanjangkan untuk memasukkan keratan rentas 4 (A₄) dan 5 (A₅), isipadu daripada CS3 ke CS5 (V_3-5) diberikan oleh:
  
  
  V_3-5  =  d  ( A₃  +  4A₄   +  A₅ )
            3
  
  
  Oleh itu, jumlah isipadu dari CS1 ke CS5 (V) ialah:
  
  
  V  =  d ( A₁  +  4A₂ + 2A₃ + 4A₄ + A₅ )
         3
  
  
  Formula am untuk N keratan rentas di mana  N mesti ganjil adalah seperti berikut:
  
  V = d  ( A₁ +A_N + 4Σ luas genap + 2Σ luas ganjil )
      3

  KAEDAH KELUASAN HUJUNG (END AREA)

• Kaedah ini sama dengan kaedah mencari keluasan dengan menggunakan Peraturan Trapezoid.
  
  

• Kaedah keluasan hujung akan memberikan keputusan yang tepat jika luas keratan rentas adalah dari magnitud yang sama.
  
  

• Jika dua keratan rentas A₁ dan A₂ mempunyai jarak mengufuk d1 antara kedua-duanya, isipadu (V₁)yang terkandung di antara dua keratan rentas diberikan oleh:    
  
  
  V₁  =  d₁ [ ( A₁ + A₂ ) / 2 ]
                     
  
  Ini membawa kepada formula umum bagi satu siri keratan rentas
  
  
  V_jumlah  =  V₁ + V₂ + V₃ + .... + V_N-1

           =  d₁ [ ( A₁ + A₂ ) / 2 ]  +  d₂ [ ( A₂ + A₃ ) / 2 ]
                                            
             + d₃ [ ( A₃ + A₄ ) / 2 ] + ... + d_N-1 [ (A_N-1 + A_N) / 2 ]
                          
  dan jika  d₁ = d₂ = d₃ = d_N-1 = d
  
  
  Jumlah isipadu =  d  [ A₁ + A_N + 2 (A₂ + A₃ + .... A_N-1) ]
                       2
  
  Kaedah ini akan memberikan keputusan yang tepat jika luas keratan rentas adalah daripada magnitud yang sama.